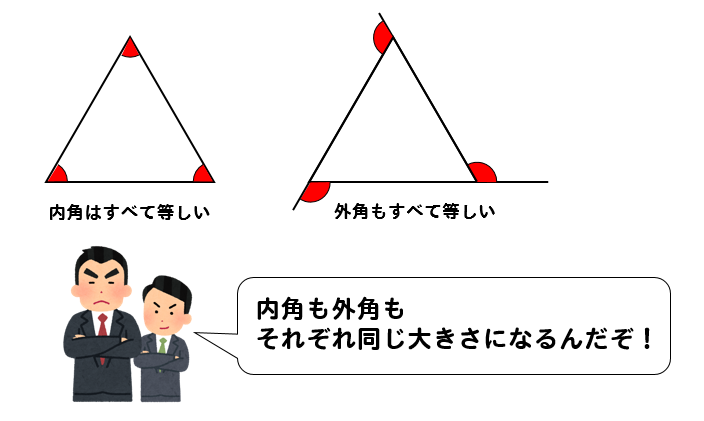
(3) 十六角形の外角の和は何度か。 (4) 十八角形の外角の和は何度か (5) 内角の和が2340°である多角形は何角形か。 (6) 内角の和が1800°である多角形は何角形か。 2410 多角形の内角と外角の和 a 30° b c 2 それぞれの正多角形について、下の表の空らんをうめ・ 四角形や五角形、六角形 など多角形の内角の和は 何度であるかを指摘でき る。 ・ 三角形の3つの角の大き さの和は180°であること を理解している。 ・ 四角形や五角形、六角形 など多角形の内角の和は 三角形の内角の和をもと にすれば求められること正十八角形において >内角の和が外角の5倍である多角形は何角形か教えてください 内角と外角の和が180度であることを使って内角と外角を求めてみよう。 そのあとに公式を使ってnに関数する方程式を作ればいいね 匿名 より 19年10月14日 314 PM いつも
2
八角形の内角の和は何度
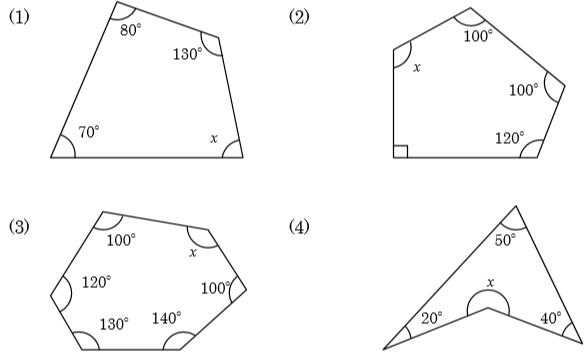
八角形の内角の和は何度-⑴ 八角形の内角の和は何度か求めなさい。 ⑵ 内角の和が 1440° である多角形は何角形か求めなさい。 ⑶ 正九角形の1つの内角の大きさを求めなさい。 ⑷ 三十角形の外角の和は何度か求めなさい。 ⑸ 正十二角形の1つの外角の大きさを求めなさい。十角形の内角の和は何度ですか。 答え (2) 正八角形の1つの内角は何度ですか。 答え (3) 内角の和が1800°になる多角形は何角形ですか。 答え (4) 十二角形の外角の和は何度ですか。 答え (5) 正十角形の1つの外角は何度ですか。 答え xの大きさを求めなさい。



八角形の内角の和は 何度ですか なんでピザみたいに中心 Yahoo 知恵袋
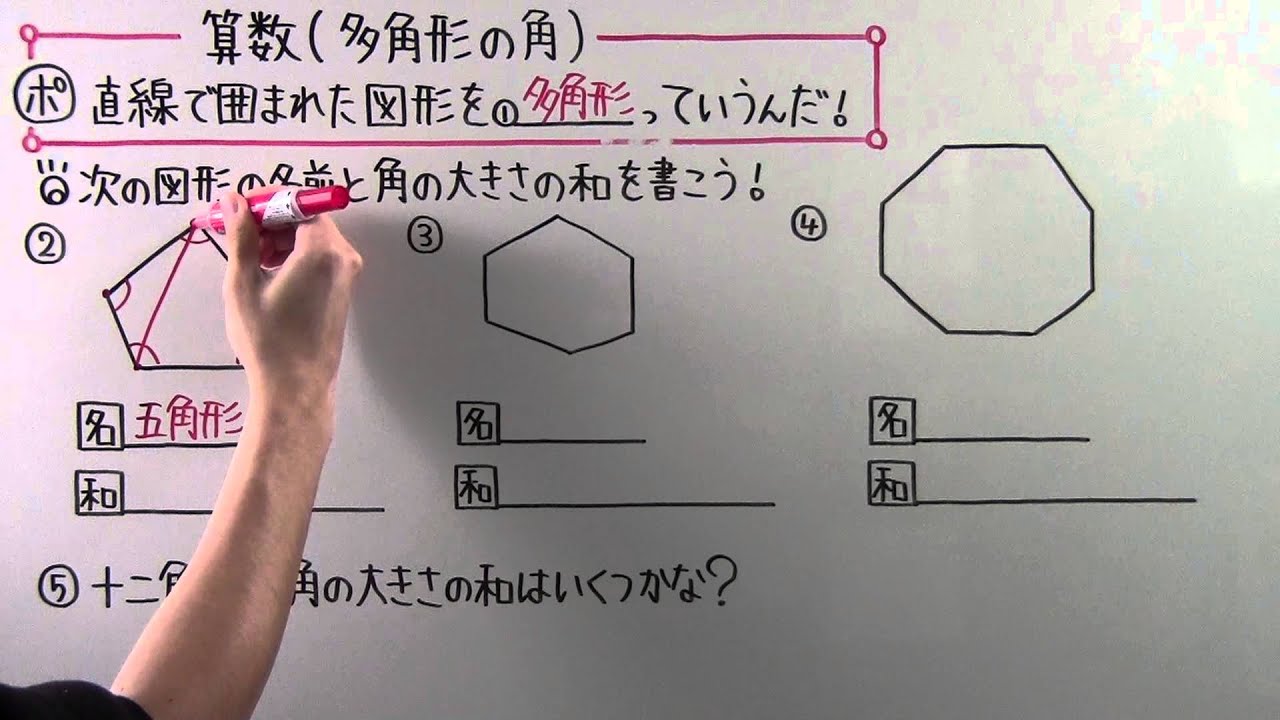
多角形の外角の和 360度 正八角形の一つの内角の大きさ 180-45=135度 確認事項:多角形の内角の和 公式は意味を理解していれば、自分で作ることが出来ます。 今回の「多角形の内角の和」も、まずは 三角形の内角の和 → 180 1 四角形の内角の和 → 180 2 五角 多角形の内角の和はそれぞれ上図の通り。 ○角形の○の数字を 2 2 で引いて 180° 180 ° をかけたものが内角の和になります。 _____ 多边形内角和=180°*(边数2) =180°*() =180°*6 =1080° 答标准8角形的角度一共是1080° 八角形的角有多少度呢 _____ 八边形是数学中的一种图形,由八条线段首尾相连围成的封闭图形,它有八条边、八个角八边形可分为正八边形和非正八边形八边形的内角和是1080
(1)九角形の内角の和は何度ですか。 (2)正五角形の1つの内角は何度ですか。 (3)1つの外角が°の正多角形は正何角形ですか。 (4)六角形の対角線の本数は何本ですか。 (5)下の図のアの角度は何度ですか。 (1)正八角形の内角の和は何度でしょう? (2)正八角形の外角の和は何度でしょう? (3)正八角形に対角線は何本引けるでしょう? 解説 (1)内角の和と来たら、どんな三角形でも内角の和は180度と使っていきたいところ。(5) 内角の和が900°である多角形は何角形か。 ( ) (6) 正二十四角形の1 つの内角の大きさは何度ですか。 ( ) (7) 十角形の内角の和は何度ですか。 ( ) (8) 内角の和が540°の多角形は何角形か求めよ。 ( ) (9) 1 つの内角が1°である多角形は正何角形か求めなさい。
星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して①正八角形の一つの内角は何度か 正八角形の内角の和は(8‐2)×180=1080度 1080÷8=135度 ②正十二角形の内角の和は?また1つの内角は何度か? 正十二角形の内角の和は(12‐2)×180=1800度 1800÷12=150度 ③正六角形の一つの外角は何度か 360÷6=60度(5) 内角の和が900°である多角形は何角形か。 180 n についての方程式ね( ^o^)φ ※これは「正」はいらないよ!問題文をよく見てね→ ( 七角形 ) (6) 正二十四角形の1 つの内角の大きさは何度ですか。 180 これを24に分ければいいね♪ ( 165° ) (7) 十角形の内角の和




十八角形 Wikipedia



八角形の内角の和は 何度ですか なんでピザみたいに中心 Yahoo 知恵袋
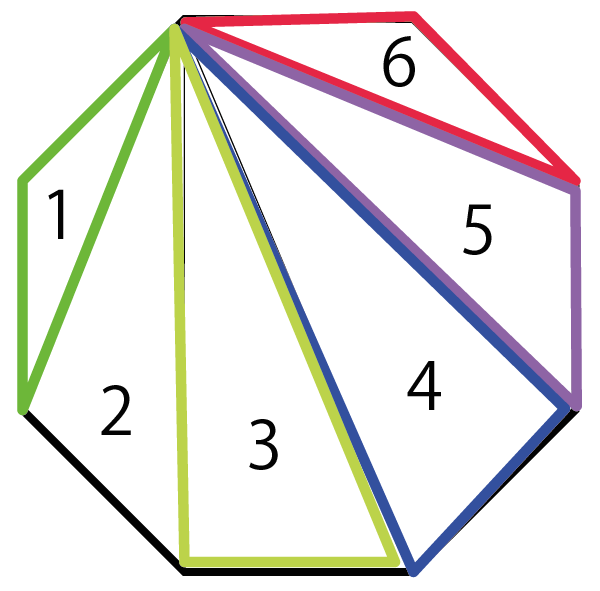
・内部に作成できる三角形の数:n-2=5-2=3個 540度 どうですか?五角形の内角の和は540度で間違いないですよね? したがって、 となるのです。これが 公式 ですよ^^八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;⑵ 八角形の内角の和は何度ですか。 (日出学園) 〔 〕 ⑶ 正十五角形の1つの角の大きさは何度ですか。 (渋谷教育学園渋谷) 〔 〕 ⑷ 次の角x,角y の大きさを求めなさい。 ① (成蹊) ② (近畿大学附属) ③ (金城学院)



720度 星形九角形の角度の和




正多角形の1つの内角 外角を求める方法を問題解説 数スタ
正十角形には,内角が10個あります。 なります。 次に,「外角の和」から求める方法を解説していきます。 外角の和は,何角形であっても,必ず360度です。 正十角形も,やはり外角の和は360度です。 正十角形には,外角は10個あります。角 X=黄色の三角形の他の2つの内角の和 対頂角は等しいから,他の2つの内角は85°と40° 角 X=85°40°=125°⑴ 八角形の内角の和は何度か求めなさい。 ⑵ 内角の和が 1440° である多角形は何角形か求めなさい。 ⑶ 正九角形の1つの内角の大きさを求めなさい。 ⑷ 三十角形の外角の和は何度か求めなさい。 ⑸ 正十二角形の1つの外角の大きさを求めなさい。




多角形の内角の和 Takapの数学日記



720度 星形九角形の角度の和
算数図形編 でる度⇒ ★★ 《角度》 多角形の内角の和を使おう 下の図は正八角形,正方形,正三角形を組み合わせた図形です。 角(あ)の大きさは何度ですか。四角形 2 五角形 540 ° 六角形 式4 七角形 900 ° 八角形 2 円の中心のまわりの角を 6等分し て、正六角形をかきました。 ①(あ)の角は何度ですか。 式 答え( ) ②(い)の角は何度ですか。 式 答え( ) ③ 正六角形の角の 1 つになってい る 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。 正多角形の内角 を知りたいときってあるよね?? 多角形の内角の和は公式つかえばドヤ顔できるけど、 せ、正多角形の内角はどうすれば・・・?
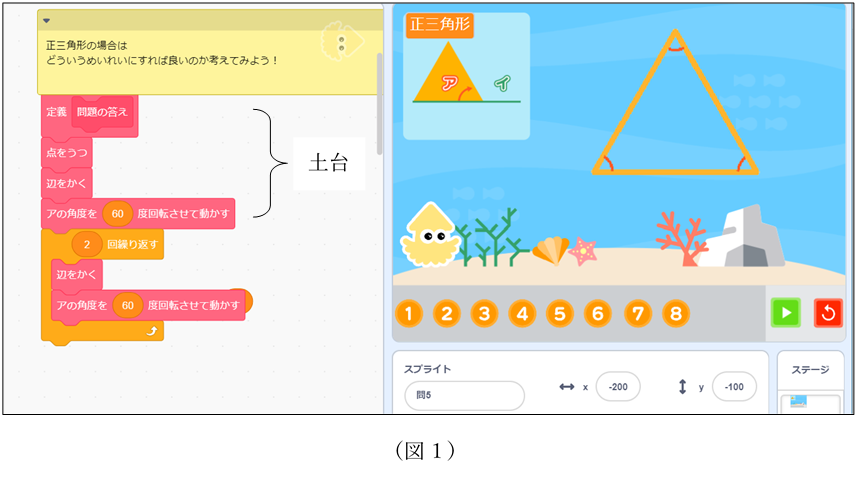



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく
数ス ② 正n角形の外角を求めて180 から引く。 ここでは②のやり方で求めてみる。多角形の外角の総和はいつでも360 であり、正多角形の場合すべての 八角形の内角の和は、1080度です。 n角形の内角の和は、 (n2)×180度で得られます。 ピザのカットで考えられてる場合、中心の先端角合計360度が 内角から除外されてることをお忘れになってます。 =1080度ですね?〔課題1〕次の多角形の内角の和は,それぞれ何度になるでしょうか。 頂点Pから対角線をひいて求め,表にまとめてみましょう。 図形 辺の数 三角形の数 内角の和




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear



1
テーマ:多角形の性質(平面図形2) レベル:2 次の図形についての問いに答えてください。 (1)正八角形の内角の和は何度でしょう? (2)正八角形の外角の和は何度でしょう? (3)正八角形に対角線は何本引けるでしょう? 基本問題八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴン チャート 」という。 世界七不思議 の一つである アレクサンドリアの大灯台 の建物は、八角形をしていたと伝えられる。十角形の内角の和は何度か。 正八角形の一つの 正多角形の1つの内角・外角を求める方法を問題解説!
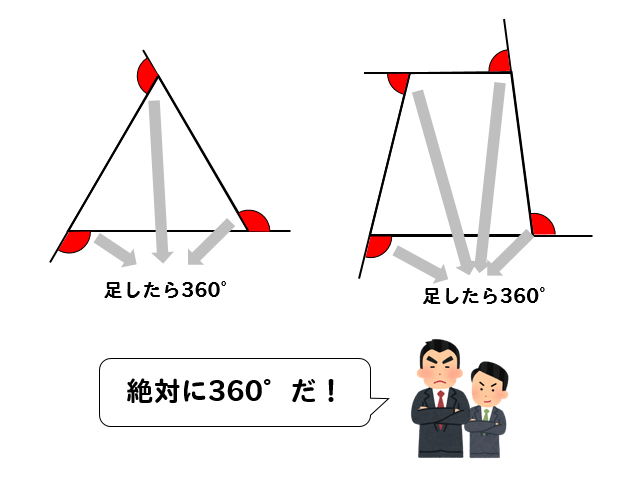



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ
正八角形の一つの内角は何度か。 次の問いに答えよ。 二十角形の内角の和は何度か。 十八角形の内角の和は何度か。 内角の和が 7°になるのは何角形か。 内角の和が 1260°になるのは何角形か。 正十五角形の 1 つの内角は何度か。 正十角形の 1 つの内角多角形の内角の和を計算します。 内角の和が1080度の多角形は、何角形でしょう? = 1080 ÷ 180 2 = 8 = 八角形 関連ページ星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e) 下の図のように,多角形の各辺を延長していくと,何回か交わったあと交わらなくなります。



一辺1の正八角形の対角線の長さを教えてください Aeの長さの出し方を教えてく Yahoo 知恵袋




多角形の内角の和 は何度なのか を説明します おかわりドリル
正八角形の内角の和は、 6 つの三角形の内角の和の合計に等しいですから、 180×6 = 1080° になります。 1つの角の角度は 1080÷8 = 135° になります。 27人 がナイス! 七角形の謎。または一周はなぜ360度なのか Updated by Ryo Shimizu on , 1102 am JST十角形の内角の和は180° (102)=1440° (4) x角形の内角の和は180° (x2)なので 八角形は180°× ()=1080°




正多角形の内角と外角の大きさ 具体例で学ぶ数学
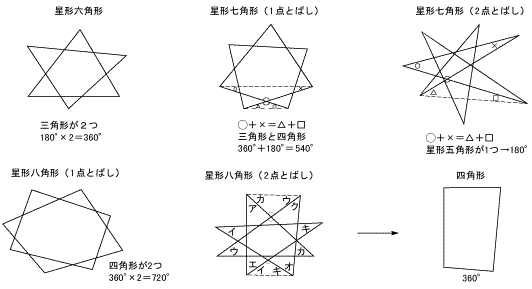



課題学習の指導 数学
三角形の性質 (3)三角形の3つの内角の和は180°である。 三角形の1つの( )は、そのとなりにない2つの内角の和に等しい。 2 次の角の大きさを求めなさい。(5問×10点) (1)正六角形の1つの内角の大きさは何度ですか。(1)八角形の内角の和は何度ですか。 (2)正九角形の1つの内角の大きさは何度ですか。 (3)七角形には,対角線が全部で何本ありますか。 例2 次の図で,同じ印をつけた角の大きさが等しいとき,角xの大きさを求めなさい。月 日 組 名前 点 三角形や四角形の角 1② ₁ 三角定 じょう 規 ぎ の角の大きさは,それぞれ何度ですか。



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 2b4 3 Pdf
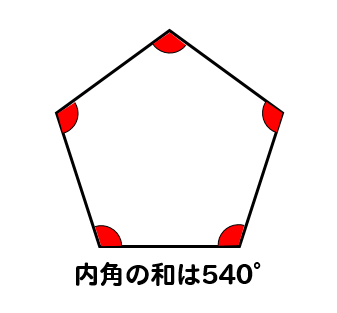



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を




多角形の内角の和 中2数学 Youtube



720度 星形九角形の角度の和



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf



Mathematics 算数のコツ 1 角度の問題は 等しい角を見つけて書き込む 働きアリ The 2nd



2




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 は何度なのか を説明します おかわりドリル




なんで かっこ1番nー2 15なんですか Clear
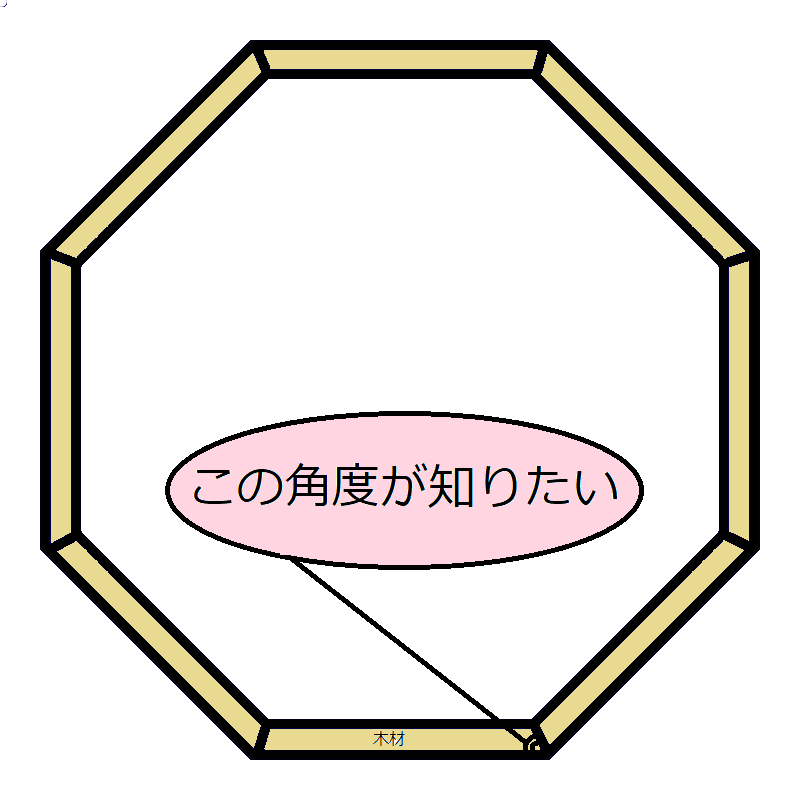



Diy ビニールハウスを作ろう Part4 By Cha Chan Potaru ぽたる



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




小5 算数 小5 54 正多角形 Youtube




中学2年の数学 動画 多角形の内角と外角の和 計算編の問題 19ch



十八角形 Wikipedia




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




八角形 Wikipedia




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




内角の和 180 N 2 外角の和 360 教遊者




九角形 Wikipedia



内角の和が540 7 900 1080 1260 の多角形は何角形か




多角形の内角の和 外角の和の公式 数学fun



Http Www Asahikawa Hkd Ed Jp Nagayama Jhs 221 Ef 92 E5 B9 B4 E6 95 B0 E5 Ad A6 Ef E5 9b E5 80 80 E5 9a E8 92 E5 81 Ae E5 86 85 E8 92 81 A8 E5 96 E8 92 80 80 E8 A3 E7 Ad 94 Ef Pdf



七角形の謎 または一周はなぜ360度なのか Wirelesswire News ワイヤレスワイヤーニュース




多角形の内角の和 算数の公式覚えてますか




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




正多角形の1つの内角 中2数学 Youtube
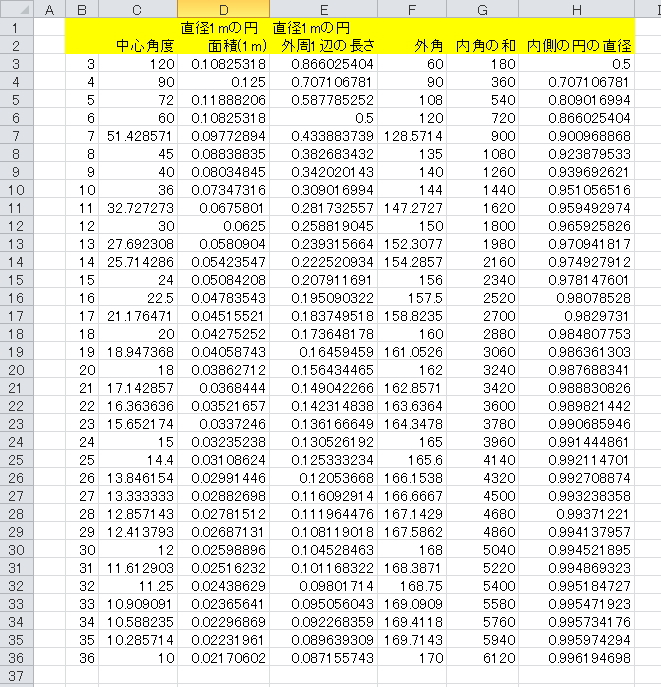



正 角形 正多角形 を表にしてみる エクセル関数の使い方
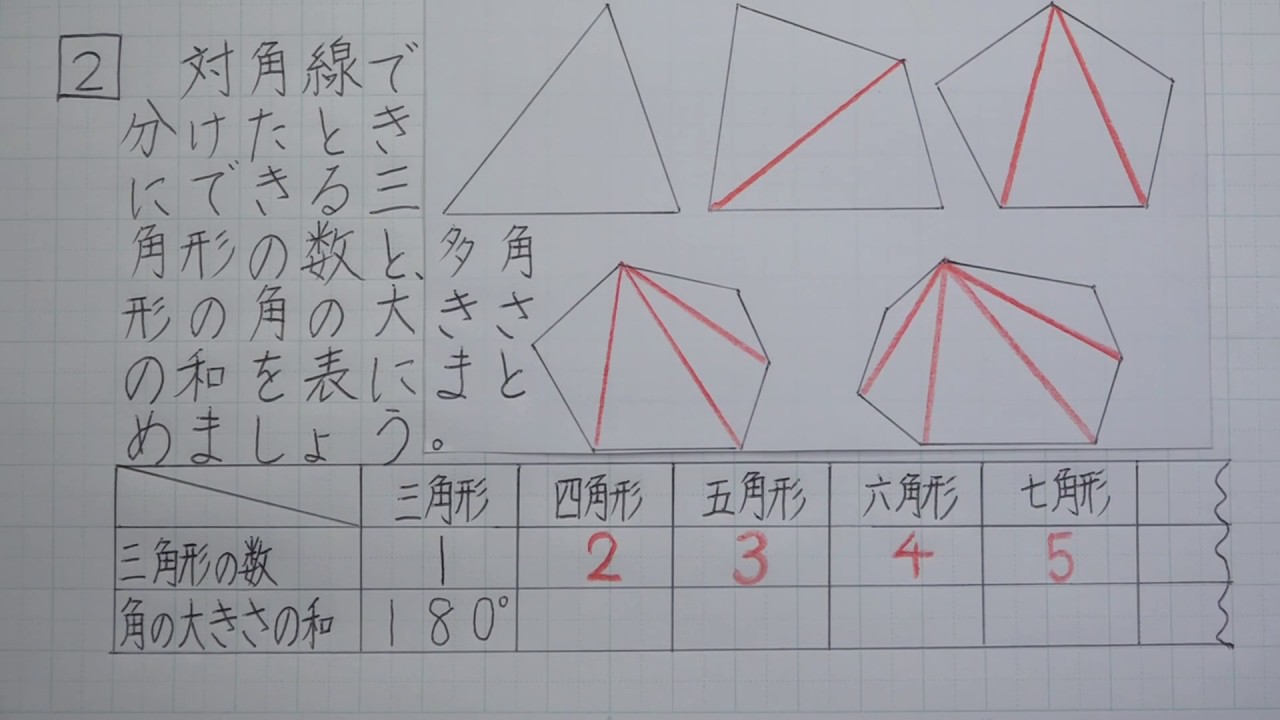



旧バージョン 5年算数 図形の角と合同 8 多角形の角の大きさの和を調べよう Youtube




6 3 4 Lihat Cara Penyelesaian Di Qanda



Www Kyo Kai Co Jp Img Material Chuu 38s Kw S2 Mihon Pdf




内角の和 180 N 2 外角の和 360 教遊者
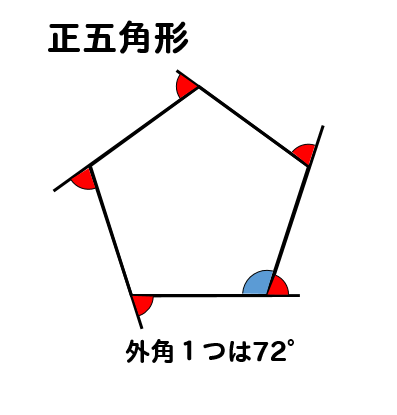



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 算数の公式覚えてますか




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学
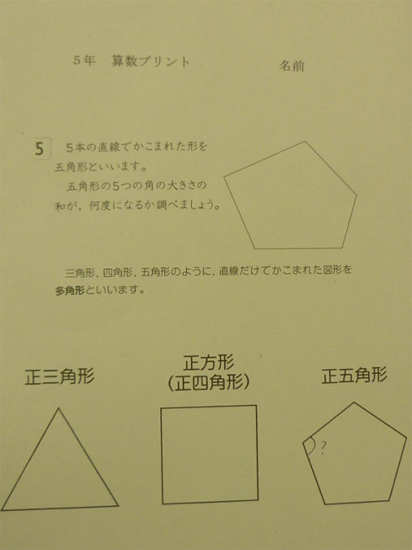



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




内角の和 180 N 2 外角の和 360 教遊者



1



2



小学校6年生の算数ですが 画像の図形の印の付いた部分の角度の合計を求め Yahoo 知恵袋




内角の和 180 N 2 外角の和 360 教遊者
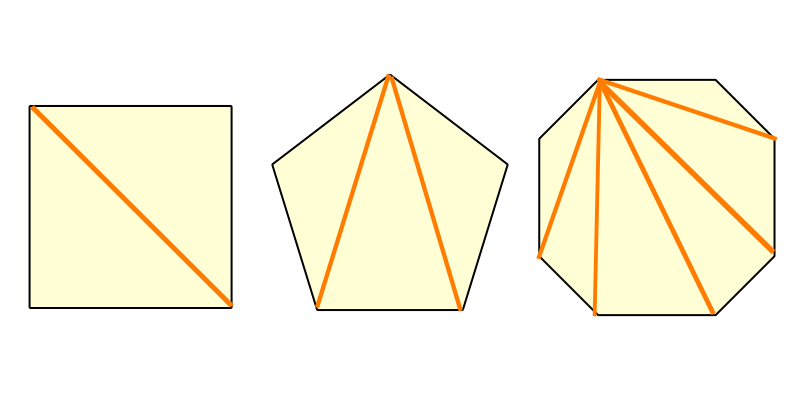



多角形の内角の和 簡単に計算できる電卓サイト




中2数学 基本解説 問題 223 図形3 多角形の角 プリント



Www City Hadano Kanagawa Jp Www Contents Simple C050a Pdf




蜀江文様 や八や八角形とは縁起モノ レトロ雑貨のブログ
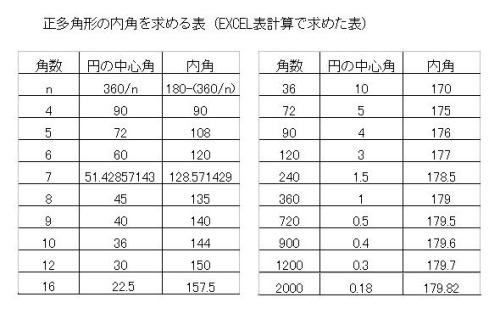



正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



小学6年生の問題です 正八角形 の1080は どうやって出た数 Yahoo 知恵袋




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




数学 中2 51 多角形の内角と外角の和 基本編 Youtube



4 1 多角形の内角の和を求めるには さんすうがく パート 2



Http Www Hpa Kb Site Com Wp Content Uploads 15 02 E5 B9 E9 9d E5 9b E5 E8 92 E5 Ba A6 8 Pdf




69の 2 100 になるらしいんだけど意味わからん Clear




一つの内角が160度である正多角形は正何角形ですか Clear



七角形の角の大きさの和の求め方を簡単に教えてください Yahoo 知恵袋




小学校5年 算数 正多角形の角の大きさ Youtube




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋



1



小5 算数 小5 33 多角形の角 Youtube



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく
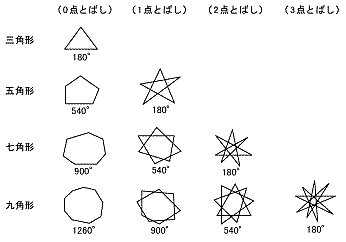



課題学習の指導 数学



みんなの算数オンライン 教科書レベル 5年 合同 三角形の内角 多角形の内角 多角形の内角 三角じょうぎ 例題と解説



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん
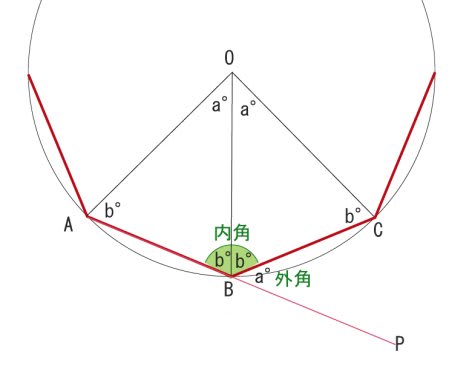



内角 外角 180 どうして 名寄 算数数学教室より
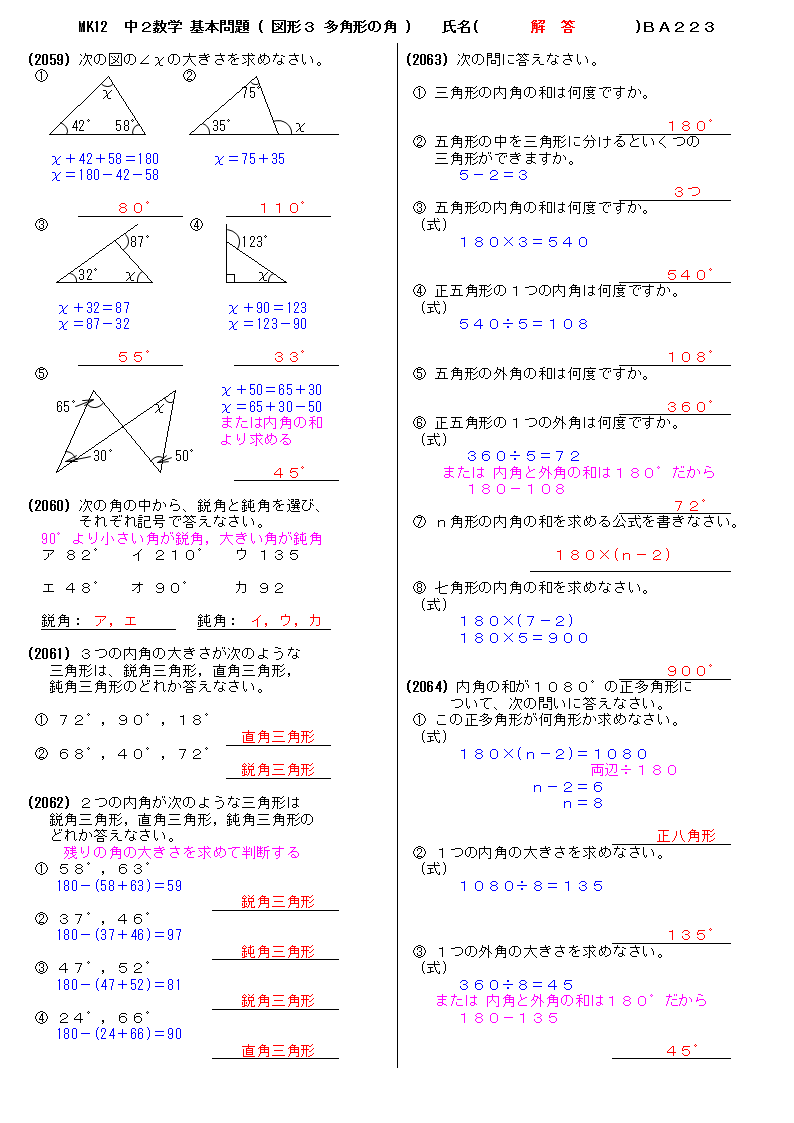



無料 中2数学 基本問題 解答プリント 223 図形3 多角形の角
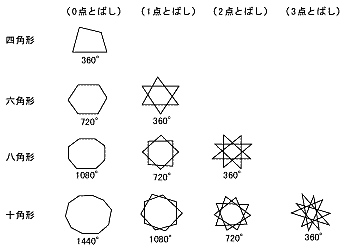



課題学習の指導 数学



Http Www Jesda Net Files Uploads E5 B9 E9 9d E5 9b E5 90 81 80 80 B5 97 Ab Pdf




数学の家庭教師 90分 サッカー個人 少人数レッスン Plus



八角形の8つの角の大きさの和は何度になりますか 公式がありま Yahoo 知恵袋




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和 外角の和の公式 数学fun




課題学習の指導 数学



Happylilac Net Seitakakkei Ans Pdf



0 件のコメント:
コメントを投稿