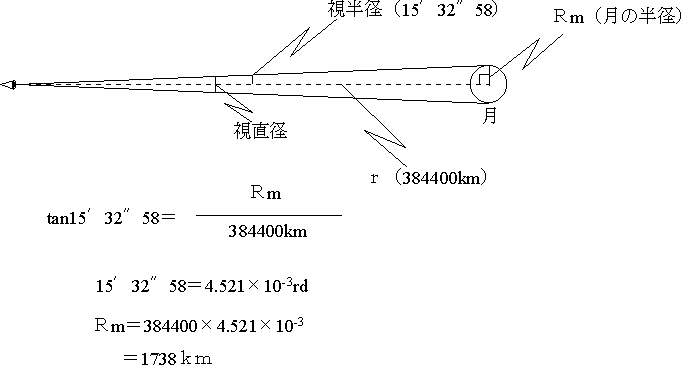
球体を切った時の直径の求め方を教えてください。 例えば、直径10センチの球が有ったとします。 この場合真っ二つにしたら、その断面の円は当然10センチですよね。 では、1センチ
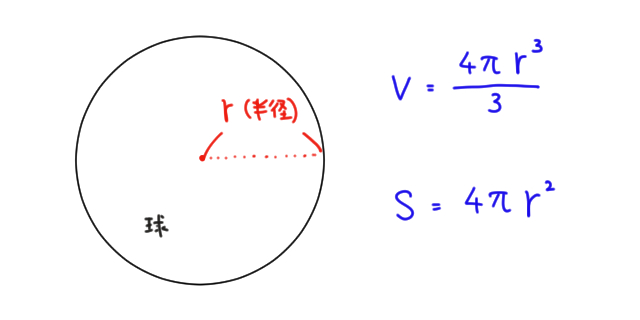
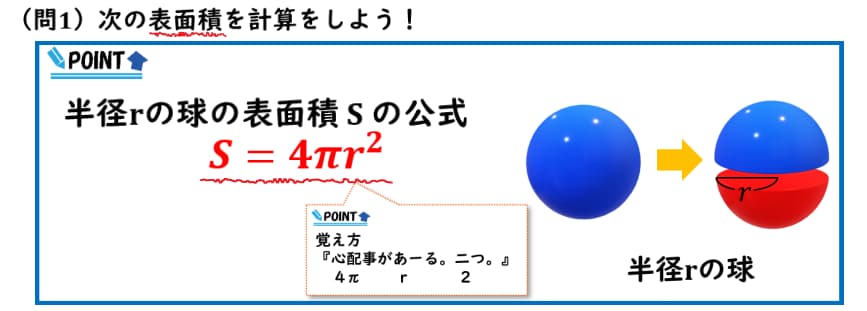
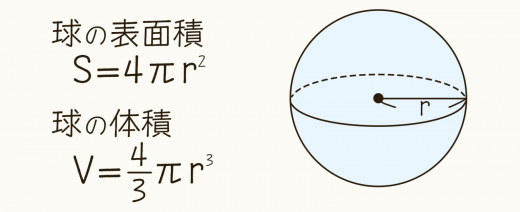
球の直径の求め方- ・球面の方程式は「x 2 y 2 z 2 +axbyczd=r 2 」か、「 (xa) 2 (yb) 2 (zc) 2 =r 2 ;中心点の座標が (a,b,c)の時」で表せる。 ・導出法は、球面と中心の長さが一定or球の直径直径から円周長 l d 円周長から直径 s d 面積から直径 長さ 円弧長 長さ h a θ s 底辺と高さ h θ b 高さ 長さ l θ h 底辺の長さ 長さ b a l 斜辺長 a θ l 斜辺長
球の直径の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | ||
 |  | 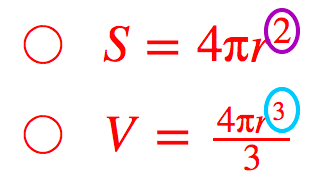 |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | 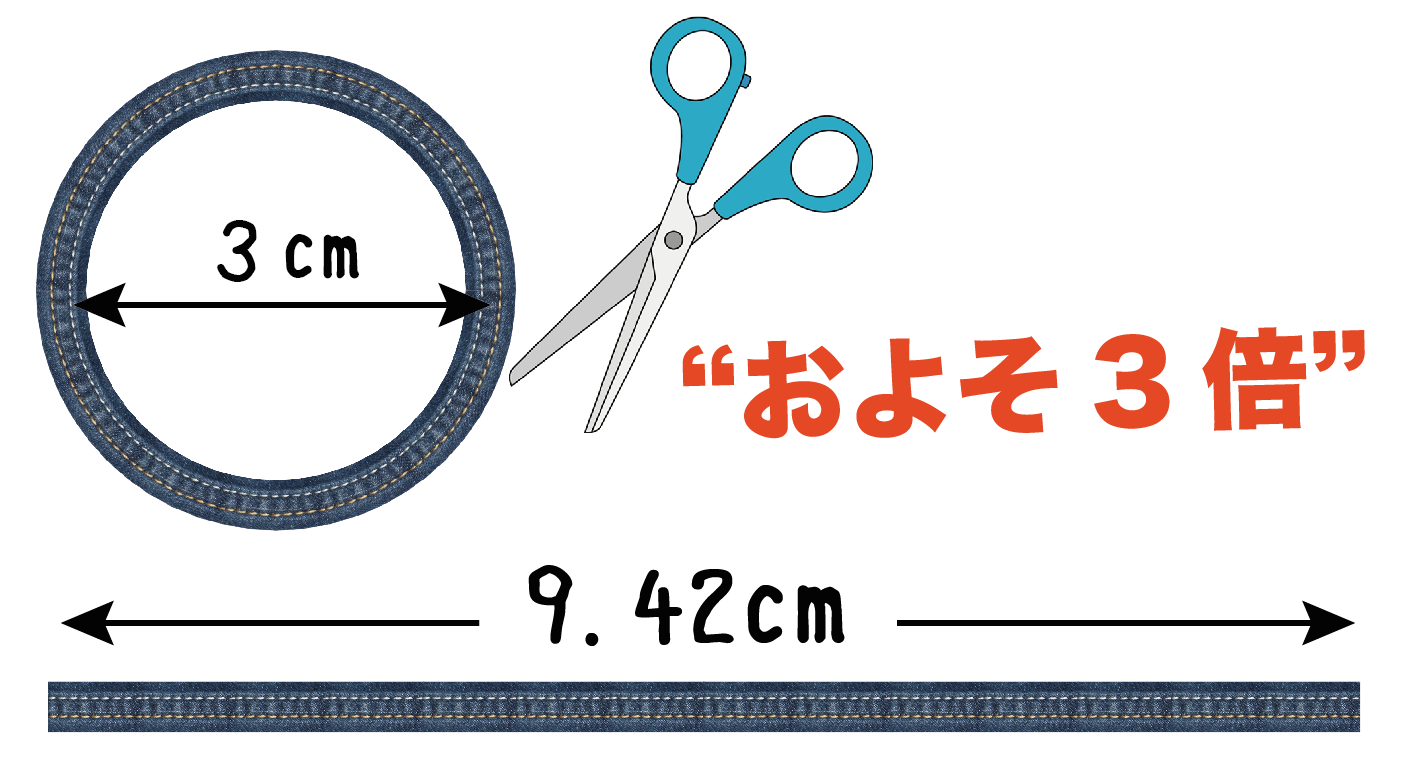 | |
 |  |  |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
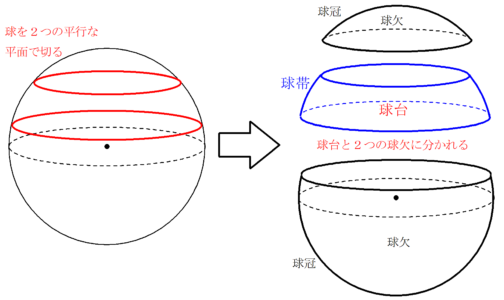
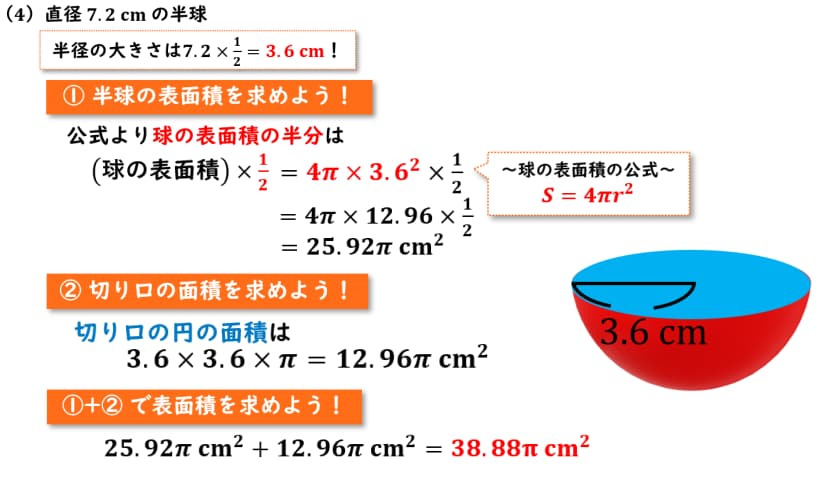 |  | 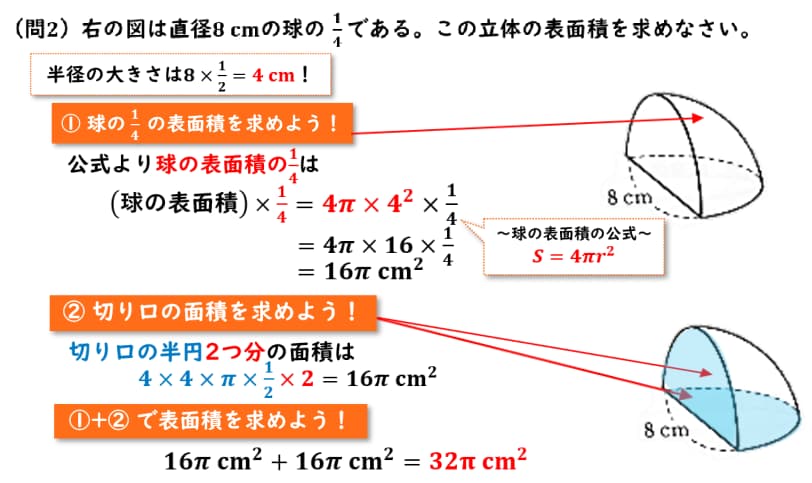 |
 | ||
 | ||
 |  | |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
「球の直径の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |
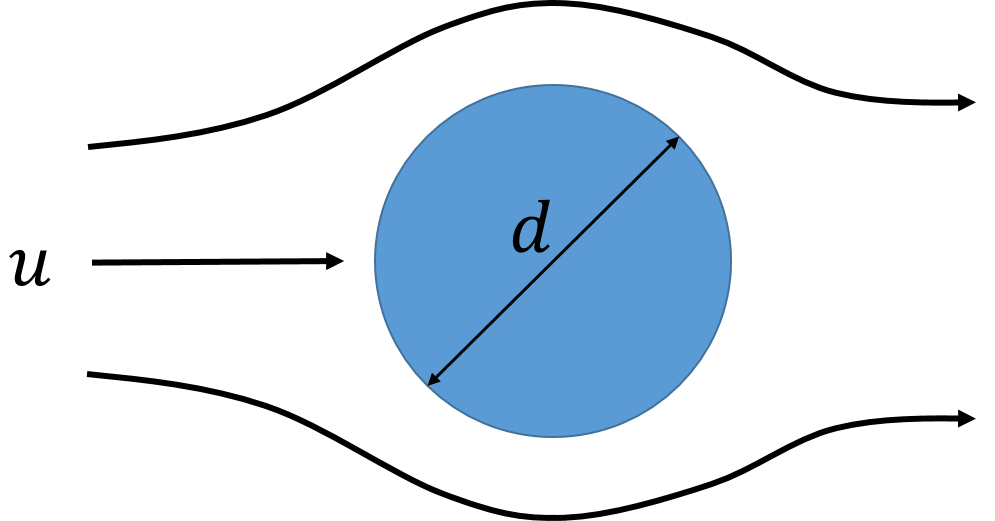
抗力係数は実験的に求められます。ρ は比質量、qは流速、Aは断面積です。球の直径をdとすると(622)式となります。 球の抗力係数の実験データ 図621において球の抗力係数は で与えられるレSΔr = (大きな球の体積)− (小さな球の体積) = 4 3π(r Δr)3 − 4 3πr3 S Δ r = (大きな球の体積) − (小さな球の体積) = 4 3 π ( r Δ r) 3 − 4 3 π r 3 が成立します。 あとは中学生でもできる(で
Incoming Term: 球の直径の求め方,




0 件のコメント:
コメントを投稿